[行业新闻] 【2011诺贝尔化学奖解读】准晶：似晶非晶

故事还要从头说起。人们早就发现，在自然界的晶体中，原子以重复的样式排列，不同的化合物也许会出现不同的排列方式，但都是简单的平移重复而已。下面是几张来自晶体中的图案模型。在图a中，我们可以看到每个原子被其他三个相同的原子包围，形成了一个单位样式，这称为三重对称，因为如果把其中之一沿着平面转过120度，将与另一个发生重叠。而在四重对称（图b）中，转过90度后可得相同图形，在六重对称（图c）中，转过60度可得相同图形。

但无论如何，五重对称（图d）却不可能得到，因为其中原子间的距离长短不一，这个样式无法实现旋转对称，由此很容易就充分证明了在晶体中找不到五重对称，依此，七重对称或者更高重的对称都是找不到的。

所以，早期晶体学家们都根深蒂固地认为，五重或七重以上的对称不符合自然规律。

然而，1982年4月的那个早晨，以色列理工学院的Daniel Shechtman 却发现在他电子显微镜下面，一个衍射图案可以安然转过圆周的1/10（也就是36度）依旧得到原来样式，也就是说，发现了十重对称！很快，他又从铝锰合金中找到了五重对称的图案。在那个时期，这项工作绝对是颠覆性的了，以至于相关论文1984年夏天被 Journal of Applied Physics 断然拒掉。还好， Physical Review Letters 没做同样的武断之事，随后就发表了他的文章。Shechtman发现的固体形态被命名为准晶（quasicrystal），以示与传统晶体的区别，并被认为是介于晶体和非晶体之间的一种形态。

事实上，无独有偶，同一时期的数学家们已为他做好了理论铺垫，英国人彭罗斯（Roger Penrose）差不多同一时期便在前人工作基础上提出了一种以两种形状的拼图铺满平面的解决方案。对于Shechtman的准晶体衍射图案和彭罗斯的镶嵌瓷砖来说，都有一个迷人的性质，就是在它们的形态中隐藏着美妙的数学常数τ，亦即黄金分割数1.618……。彭罗斯瓷砖以一胖一瘦两种菱形（内角分别为72度、108度和36度、144度）镶拼而成，两种菱形的数量之比正好是τ；同样的，在准晶中，原子之间的距离之比也往往趋近于这个值。

黄金分割数的概念早在13世纪就已经有人描述，它来自著名的斐波那契数列（1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144）,这个数列越往后，两个相邻数字的比值就越接近τ。在自然界中，这个数值和一些事物的生长形态有着神奇的联系，比如我们熟悉的向日葵盘，种子的分布就是以由黄金分割角发散呈现的，还有海螺的生长线也遵循了这一规律。

如今在钴、铁、镍等金属的铝合金中，准晶已经成为了一种见怪不怪的结构，有趣是，准晶出自合金，本身却是电的不良导体。它的其他特点包括：磁性较强，在高温下也比晶体更有弹性，十分坚硬，抗变形能力也很强，因此可以作为商用价值很好的表面涂层。目前世界上准晶的研究十分活跃，在法国、德国、日本和美国都有，预计在未来几年中，它的低摩擦、耐腐蚀、耐热性和非粘性会进一步被开发利用于材料领域，有人也在铝基体中嵌入了硬纳米准晶，去发掘它的更多性能。准晶甚至对于高维空间的探索也有其特殊的模型功用，哈佛大学理论物理学家、美女教授丽莎兰道尔（Lisa Randall）在其科普书《弯曲的旅行》中就曾写道：带有准晶体镀层的锅之所以不粘，正是利用了准晶体与常见食物的结构差异，锅里镀层大高维晶体投影与常见食物的三维平凡结构是有差异的，原子排列的不同使得它们不会粘连在一起。

关于准晶的研究方兴未艾，比如说光子准晶，它是以准周期形式排列的，和光子晶体具有相似的性质（如各向同性的带隙），可用于建造微型光学元件。

下图显示了一组光子准晶的几何构型，其中亚波长绝缘棒被以彭罗斯平铺的方式排列，背景中充满空气。

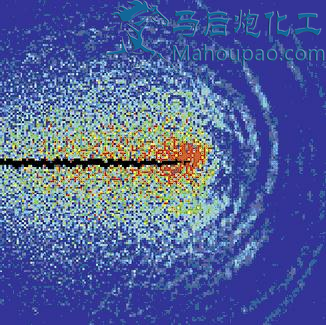
下图显示了光子准晶中谐振状态的分布强度，红色对应高强度，蓝色对应低强度（看上去真的犹如古典风的玻璃灯罩……）。

下图则显示的是与上图相同谐振状态下的相位分布。

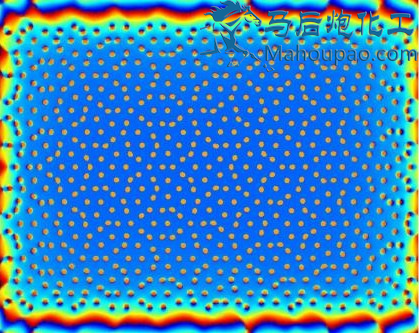
这是斯图加特大学的一个小组在二维的准晶模型进行裂纹扩展的分子动力学模拟。

在理论上，有三种准晶模型。第一种即是彭罗斯模型，是由彭罗斯以及宾夕法尼亚大学的两位科学家Dov Levine和Paul J. Steinhardt提出的，该模型中两种或两种以上的晶胞以特定规则拼接在一起铺满平面；第二种是玻璃模型，由美国物理学家Peter W. Stephens和Alan J. Goldman提出，在这种模型中原子簇可以较为随机地加入交互形成；第三种是随机平铺模型，它结合了前两种的特点，即彭罗斯模型中的规则不必被严格执行，只要结构中并没有出现间隙，晶胞自行加以组合即可。

下面是一组利用傅里叶变换做出来的各种规则的准晶图案，从上到下分别为五重、九重和十二重对称。

下面也是一组利用傅里叶变换做出来的但是随机分布的准晶图案，从上到下分别为五重、九重和十二重对称，可与上图做个比较来看。

由于准晶具有美妙绝伦的几何视觉效果，它对艺术和建筑界的启发也比比皆是，下图是日本艺术家Akio HIZUME利用510根小木杆做出来的准晶模型，叫做MU-MAGARI。